Learn Texas Holdem Video Source & Info:
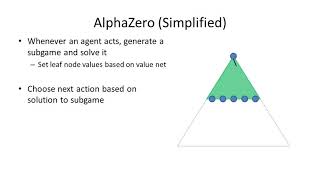
The combination of deep reinforcement learning and search at both training and test time is a powerful paradigm that has led to a number of successes in single-agent settings and perfect-information games, best exemplified by AlphaZero. However, prior algorithms of this form cannot cope with imperfect-information games. This paper presents ReBeL, a general framework for self-play reinforcement learning and search that provably converges to a Nash equilibrium in any two-player zero-sum game. In the simpler setting of perfect-information games, ReBeL reduces to an algorithm similar to AlphaZero. Results in two different imperfect-information games show ReBeL converges to an approximate Nash equilibrium. We also show ReBeL achieves superhuman performance in heads-up no-limit Texas hold’em poker, while using far less domain knowledge than any prior poker AI.
Noam Brown*, Anton Bakhtin*, Adam Lerer, Qucheng Gong
NeurIPS 2020
https://arxiv.org/abs/2007.13544
Source: YouTube







Thank you for the video! I'm an undergraduate who wants to learn a lot more about RL, and this was really great. I was actually curious whether ReBeL could be directly applied to a game like Pokemon. I'm not sure how familiar you are with battling mechanics in Pokemon, but there is a lot of imperfect information (each opponent Pokemon has hidden moves, hidden stats which can later be inferred based on observable damage numbers and moves used) as well as damage rolls, crits, etc. In particular, unlike poker or RPS where there is a set turn order (for RPS we reformulated it to be this way), in Pokemon move order is determined by speed stat of the Pokemon in play, which is sometimes hidden to the players if not previously observed. Would you still be able to use ReBeL in this case, and would it have to be reformulated in any way?
Also, I just had a couple quick clarifying questions about belief infostates. You mentioned in the paper that the input of the value network is the following size:
1(agent index) + 1(acting agent) + 1(pot) + 5(board) + 2 × 1326(infostate beliefs)
Why is there a separate value for "agent index" and "acting agent"? Also, are infostate beliefs just the set of probabilities for every possible player hand (which we update based on player actions)? Why don't we include information such as amount of money each player put in the pot and bets made during that current round?
Thank you again so much for the paper and video, I appreciate your time to help people like me learn more!
This is the best ReBeL video I've watched. I'm very impressed by your insights into the method. Then I realized you are one of the authors …
The value vector computed with cfr is added as a training example. When solving the the last round, these values are completely accurate if it was solved to 0% exploitability. So over time it will get better at solving the round before the last, then the round before that. Something I don't understand is that you don't solve until the start of the next round. How does the value network improve at estimating the leaf nodes when you are giving it training data that consists only of public belief states at the start of a betting round?
Hi Noam, I think this field of research is fascinating and it's very impressive to see the strides you took and are taking in the realm of imperfect information games.
Previously, Pluribus cost very little computationally, despite being placed in a 6 person table. I found one of the most impressive stats of Pluribus being that it only took ~$150 and a relatively weak computation to train and execute (which is because of the lack of deep neural nets?). In comparison, with the implementation of deep reinforcement and self play without information abstraction, how does ReBel compare in terms of cost and computability? Thanks
I think this technique would be applicable to tranding card games like magic or Yu-Gi-Oh but would it struggle with different matchups or decks that are not equal, and if so do you think there are ways of addressing it?
Hi Noam, I was wondering what the computational requirements of training ReBeL was as opposed to for the libratus model. I assume this is significantly more expensive considering the continuous nature of game state space, and the fact that the game state now contains atleast as much information as libratus's game space. Could you improve my understanding of this? Thanks!
The proof of Theorem 3 is not very convincing. It looks like you are proving that the strategy obtained by Algorithm 1 is an equilibrium in a game where players know the past strategies and can compute beliefs. This is because the value at leaf nodes is obtained as a function of beta^t which in turn is a function of the strategies. Furthermore, according to the proof, the policy averaged over all iterations and the policy that stops at a random iteration are equivalent. However, you seem to imply that one of them works while the other does not. There seems to be a discrepancy here, it would be great if you can clarify this.
In zero-sum games, going from the case where the strategies are common knowledge to the case where they are not common knowledge is a tricky long-standing problem that has been addressed only in some special cases. That is why I feel skeptical about Theorem 3 and I think it should be handled more carefully.
Hello! I am wondering how exactly a subgame is constructed from a PBS. At first I thought that you would just sample an infostate for each player using the infostate probabilities, and then construct a subgame in the discrete representation using those infostates, but then I realized this doesnt work because some infostates may be incompatible (eg both players cannot hold the same card in poker).Thanks in advance!
I just read "Superhuman AI for multiplayer poker" article by this Noam Brown guy and became interested in the "Supplementary Materials" he published for this project- but barely understood things.
Then I open up youtube to introduce myself to Monte Carlo CFR and find this… Thank you in advance already!
For the turn endgame holdem experiment where you trained with random values – Was this something like each of the possible hands has a random probability between 0 and 1? I was able to train a river net to a training loss of 0.013 and validation loss of 0.018 with 500k samples (solved to an exploitability of 0.1% of the pot) using Deepstack's pseudorandom range generating function and having the board be an input to the network (represented as 52 0's or 1s depending on if the card is on the board). The inputs were also players ranges rather than bucket probabilities. I also tested the network in different situations where both players had 100% of possible hands (a distribution not represented in the data), and it had a loss of about 0.003 in those cases (albeit a small sample). For some reason, that is an easier distribution than the pseudorandom distribution.
I'm guessing that if you assign random probabilities to every hand – each hand strength is going to have a similar number of combos in most samples. For instance, there may be 100 hands that make top pair, most samples on that board are going to have around 50 combinations of top pair. It may not be able to generalize in situations where a hand strength is very unlikely or very likely. I've come to the conclusion that buckets were not necessary in Deepstack or Supremus, but the algorithm for generating players ranges is.